Back

Breadth-First Search Algorithm

12 Oct 2018

Breadth-First-Search is a graph traversal algorithm.

You might ask, what is Graph Traversal? The process of visiting each node/vertex in a graph is called - graph traversal. The order in which these vertices are visited determines what algorithm we use to traverse a graph - Breadth First Search(BFS) or Depth First Search(DFS)

In this post, we will go into the details of BFS.

What is BFS traversal?

BFS algorithm traverses broadly or width-wise. It visits it’s neighbors before visiting the children and uses Queue data structure.

BFS traversal explanation

To determine the unvisited, visited and explored nodes, let’s give them colors.

  • black -> unvisited
  • red -> explored

Initially our graph is going to look like this. Graph

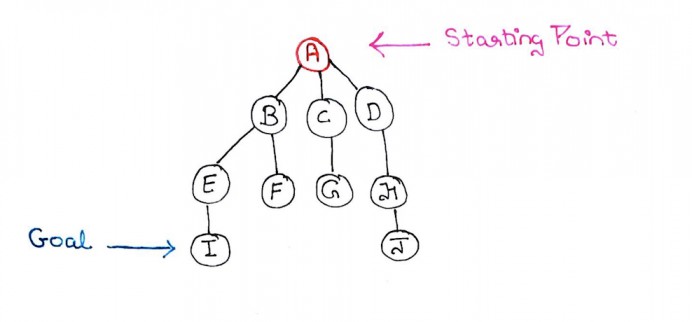
Step 1: We select our starting vertex as A and our goal as I. We want to search the nodes width-wise, till we reach point I. Step1

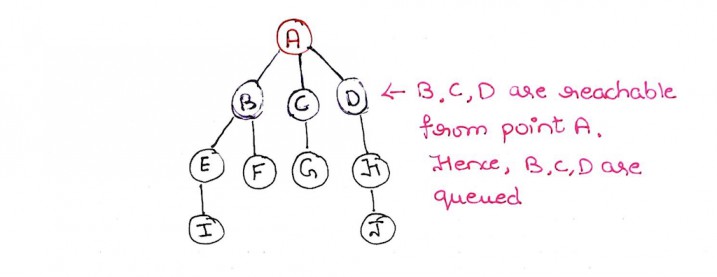
Step 2: Nodes B, C, D are reachable from node A. So we mark A as explored, B, C and D as visited. Marking B, C, D visited also means that these nodes have to be queued. Step2

Step 3: Now we select node B Step3

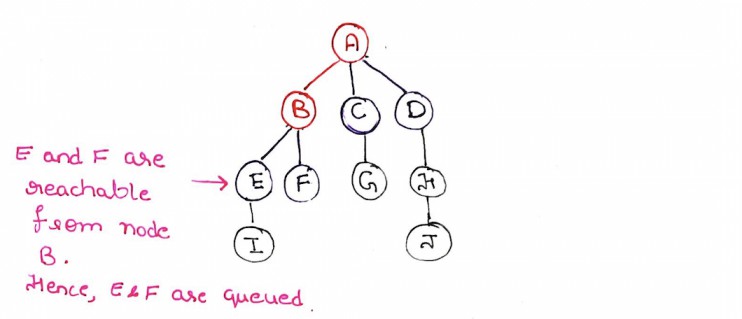
Step 4: Nodes E and F are reachable from node B. We mark them as visited and add them to the queue. We mark B as explored Step4

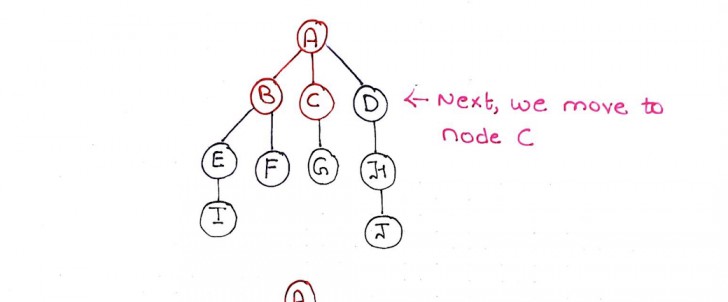
Step 5: Because there are no more nodes to visit through node B. We move on to the next queued node, which is node C. Step5

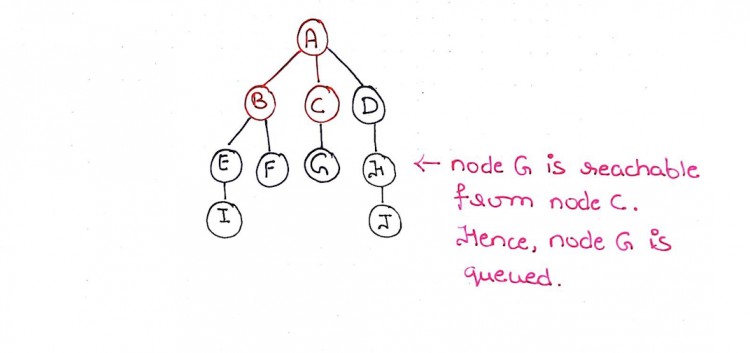
Step 6: From node C, we can reach node G. We mark G as visited and is queued. C is marked as explored. Step6

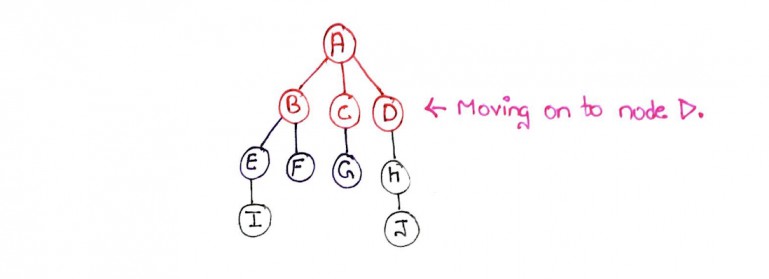
Step 7: Since, there are no more nodes to visit in node C. We move on to node D Step7

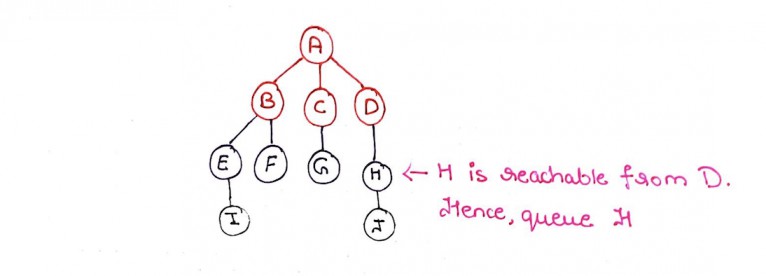
Step 8: We can see that from node D, node H is reachable. So we mark node H as visited and queue it. Node D is marked as explored. Step8

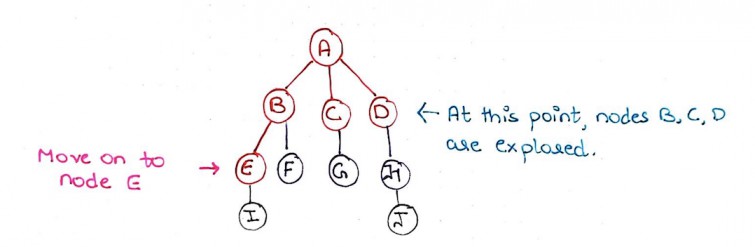
Step 9: All the nodes B, C and D at level 1 have been explored. We move on to the next queued node, which is E. Step9

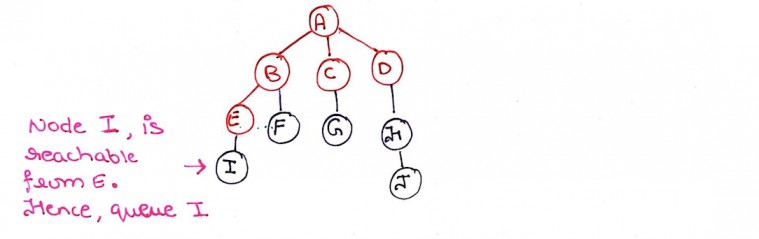
Step 10: Node I is reachable from node E. So we mark I as visited and E as explored. I is queued. Step10

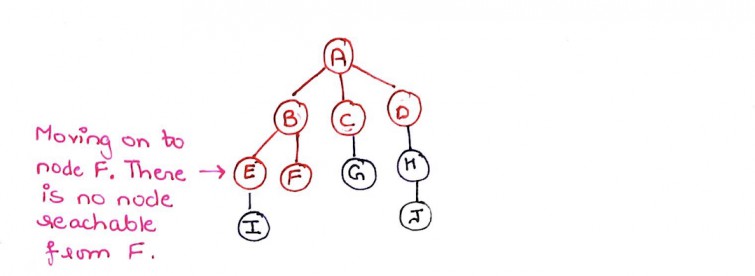
Step 11: We check node F now and observe that it has no children.So, we mark node F as explored. Step11

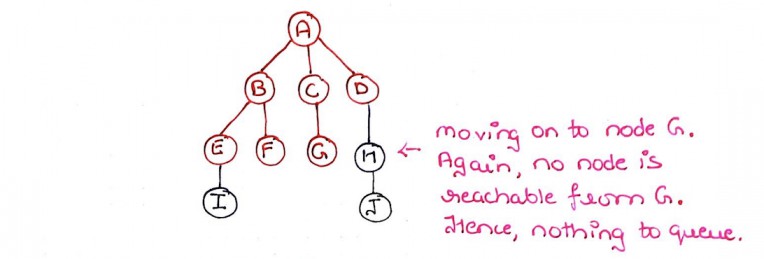
Step 12: It is the same case with node G. It has no children. so, we mark node G as explored and move on to the next queued node. Step12

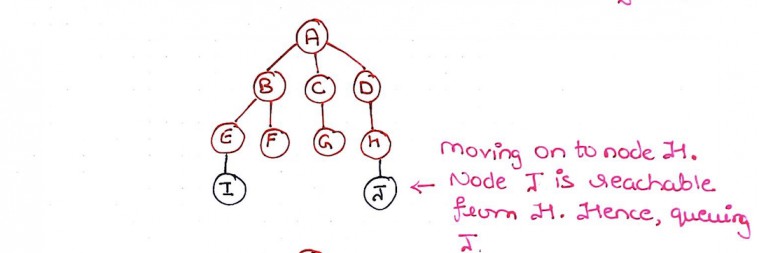
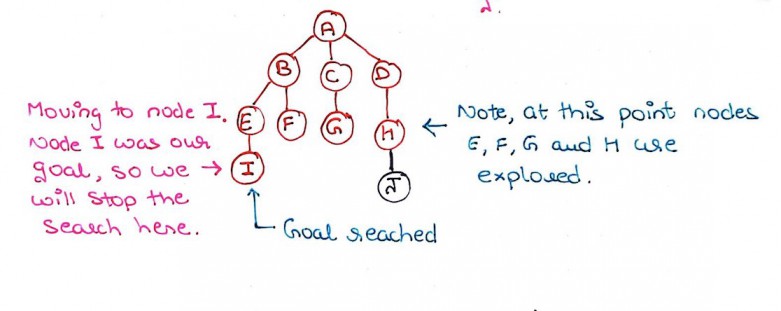
Step 13: Our next queued node is H. Here, we find an unvisited child J. So, we mark J as visited and add it to the queue. We mark H as explored Step13

Step 14: Finally, we reach node I. Node I was our goal node and we have reached it, so we abandon any further search and call our BFS successful! Step14

Algorithm for BFS

 1. Create queue
 2. Mark starting vertex(v) as discovered (grey).
 3. Enqueue v to queue
 4. Loop through queue ,while queue is not empty:
    4.1 Dequeue first node from queue, let's call it u.
    4.2 Mark u as discovered (grey). The undiscovered nodes are marked white.
    4.3 Find it's neighbors
    4.4 Loop through each neighbor. We will call each element w:
        4.4.1 Check is the neighbor(w) is undiscovered (white)
              4.4.1.1 Mark it(w) as discovered (grey)
              4.4.1.2 Enqueue the neighbor (w)
    4.5 Mark u as explored(black);
    4.6 Concatenate the result to the queue

Time and Space complexity

In BFS, we are iterating only once to find the neighbors of one vertex. Therefore, assuming that we have n nodes, every node is enqueued at least once and check the edges of adjacency list once, our time complexity will be O(V + E).

In case of undirected graph:

F(n) = Visiting vertices(V) + number of Edges(E) in adjacency list = O(V) + O(E)
	 = O(V + E)

In case of directed graph:

F(n) = Visiting vertices(V) + number of Edges(E) in adjacency list = O(V) + O(2|E|)
	 = O(V + E)

Check out the code for BFS here.

Back