Back

Depth-First Search Algorithm

26 Oct 2018

In the last blog we discussed BFS Algorithm(put link here) which is a graph traversal algorithm that traverses broadly or width - wise. In this blog I will discuss another approach or algorithm for Graph traversal - Depth First Search or DFS

What is Depth First Search Algorithm?

DFS is an algorithm that traverses the graph from top to down, or length - wise. The node visits it’s children before visiting it’s neighbors. One thing to note in DFS is that the data structure used is Stacks. Recursion uses stack, and we are using recursion for the implementation of our algorithm.

DFS traversal Explanation

To determine the unvisited, visited and explored nodes, let’s give them colors.

  • black -> unvisited
  • blue -> discovered / visited
  • red -> explored

Initially the graph looks like this.

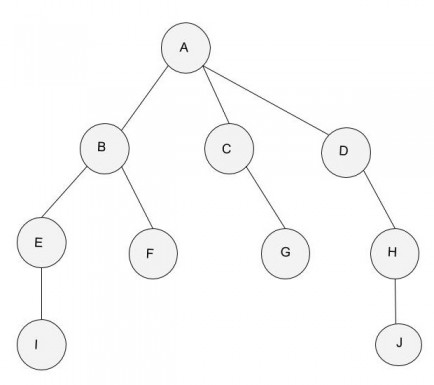
Step1

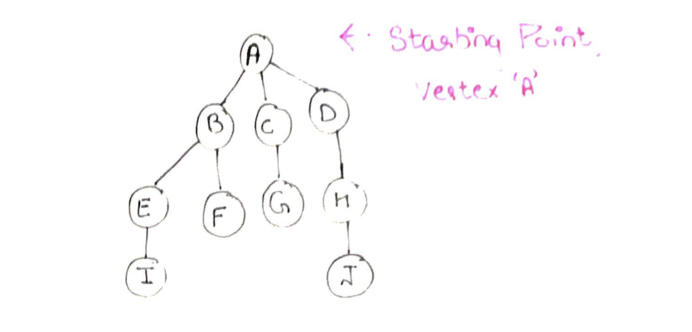
Step 1: We select our starting vertex as A. We want to search the nodes length-wise, till we have traversed the whole graph. We mark A as discovered and push it to the stack. Step1

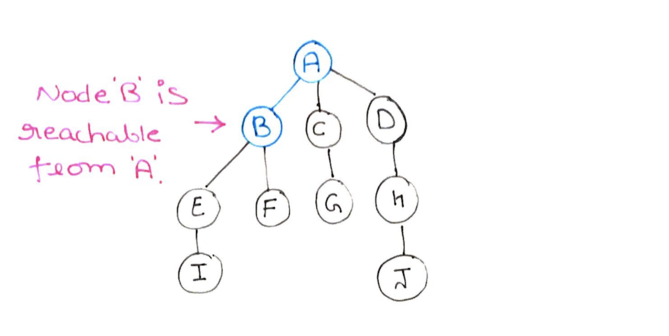
Step 2: Nodes B, is reachable from node A, hence we mark it as discovered, and push B to the stack. Step2

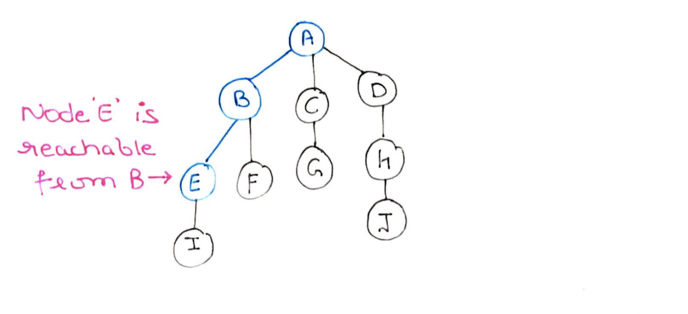
Step 3: Node E is reachable from B. So me mark E as discovered as well and push it to the stack. Step3

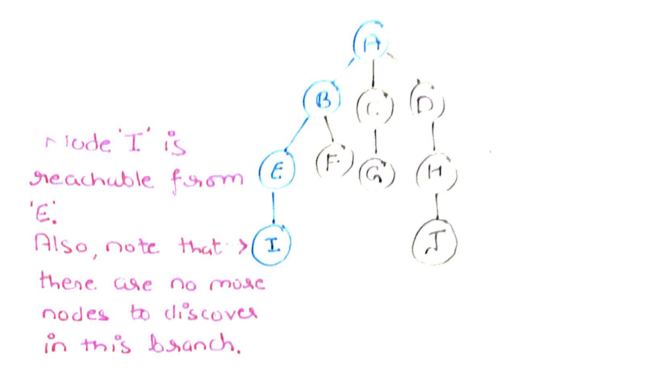
Step 4: Select node E, and we observe that node I is reachable from E. So me mark I as discovered and push it to the stack. Step4

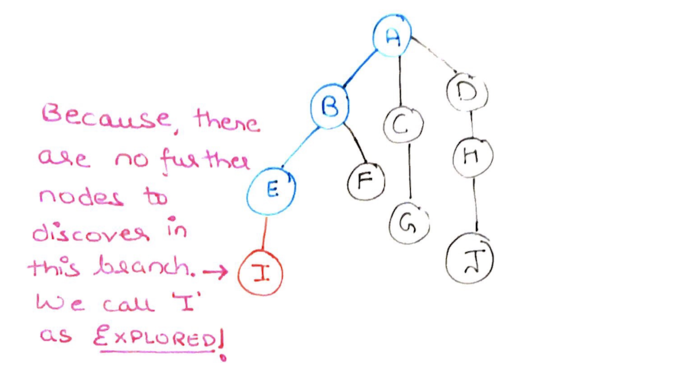
Step 5: Because there are no more nodes to visit from node I. We return it from the stack and mark it as explored(red). Step5

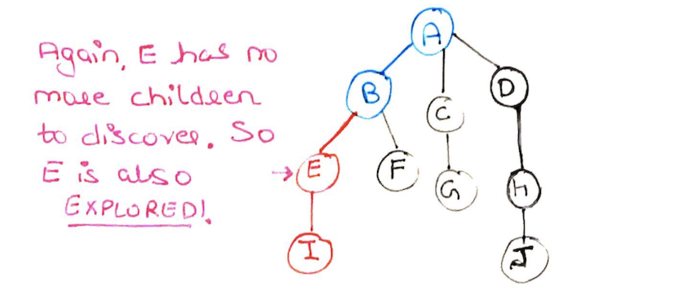
Step 6: Because there are no more nodes to visit from node E. We return node E also from the stack and mark it as explored (red). Step6

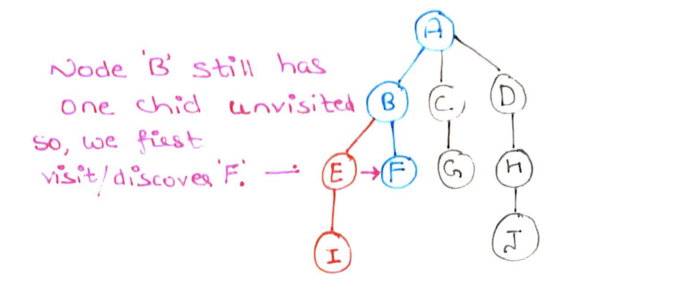
Step 7: We have reached node B and observe that node F is reachable from B. So we mark F as discovered. Step7

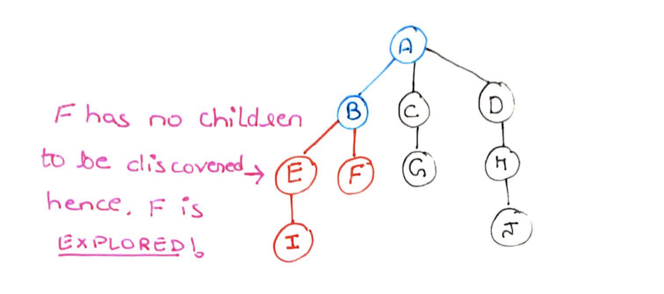
Step 8: F has no children to discover. So we return F and mark it as explored(red) Step8

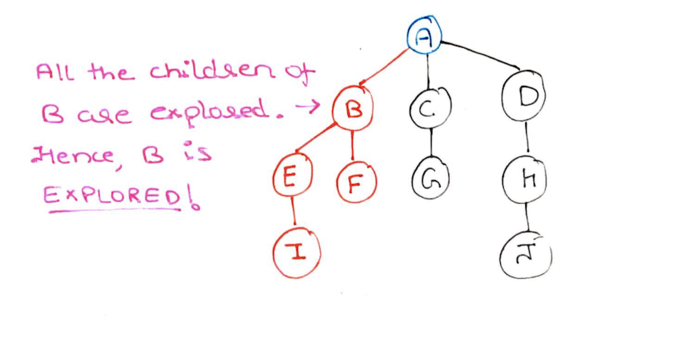
Step 9: Same with node B. B does not have any more children to discover, so we return it and mark B as explored (red). Step9

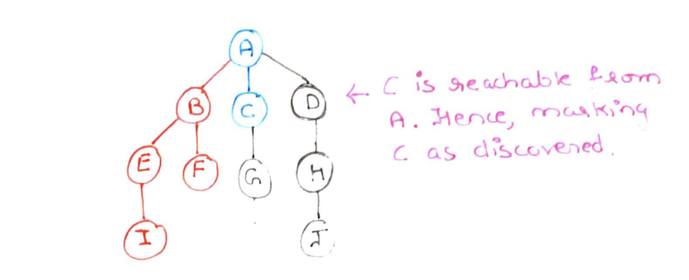
Step 10: Next we observe that C is also reachable from A. So we mark C as discovered. Step10

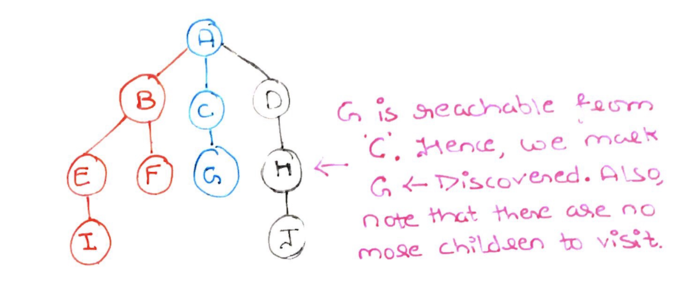
Step 11: Node G is reachable from C. So we mark G as discovered. Step11

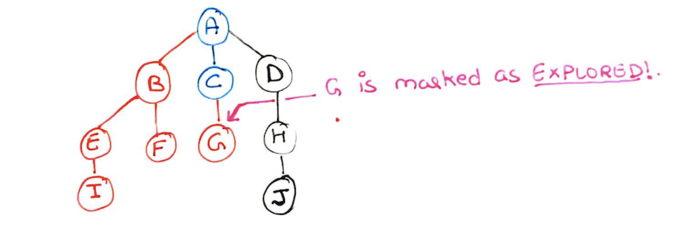
Step 12: Node G has no children to be discovered. So we return node G and mark it as explored(red). Step12

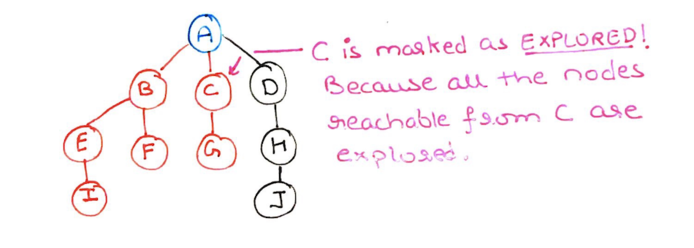
Step 13: All the children of node C has also been explored, and no other node is reachable from C. So we mark C as explored (red) and pop it from the stack. Step13

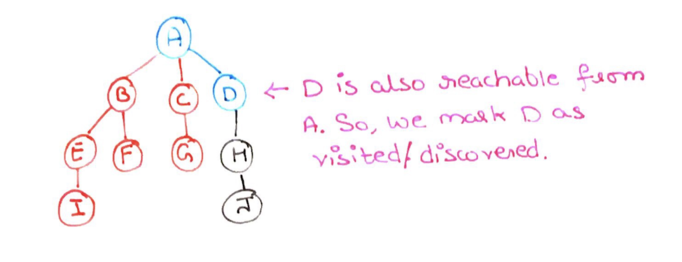
Step 14: Now we select node D, and see that node D is reachable from A. So me mark D as discovered. Step14

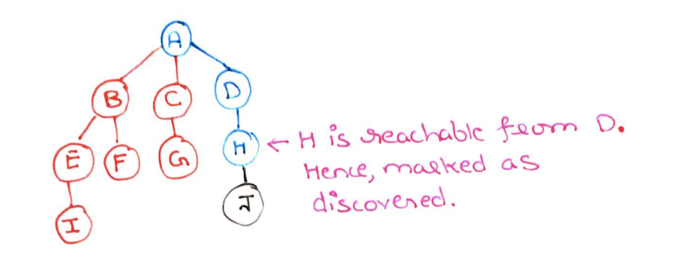
Step 15: Now we select node H, which is reachable from node D. We mark H as discovered. Step15

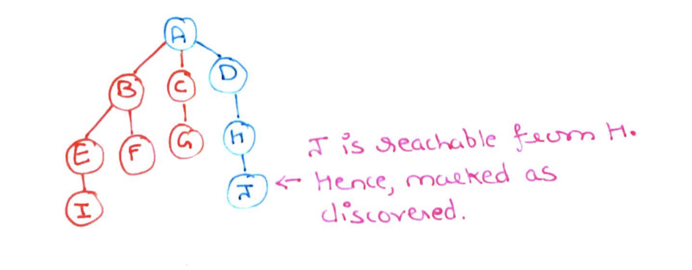
Step 16: Similarly for node J. We observe that J is reachable from H and mark it as discovered. Step16

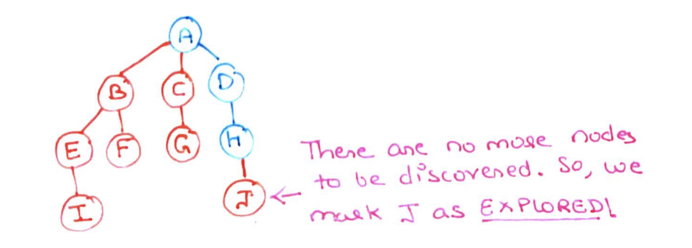
Step 17: Because there are no more nodes to visit from node J. We return it from the stack and mark it as explored (red). Step17

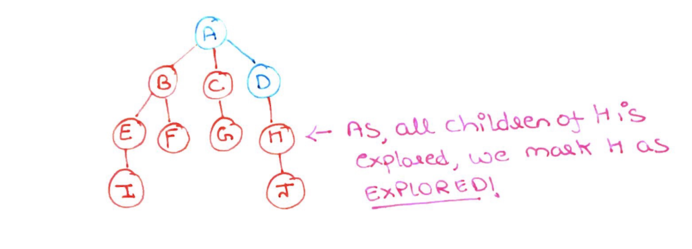
Step 18: Same with node H. There are no more nodes to be discovered from H, so we mark it as explored (red) and return it from the stack. Step18

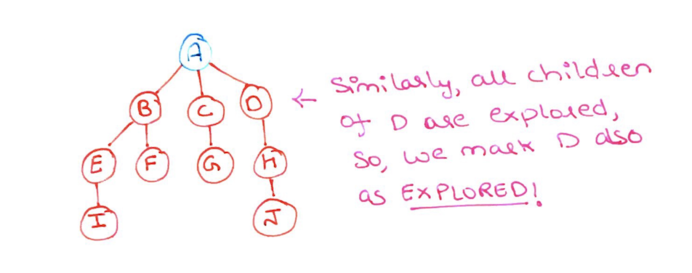
Step 19: D also has no children left to be discovered. So we return D and mark it as explored (red) Step19

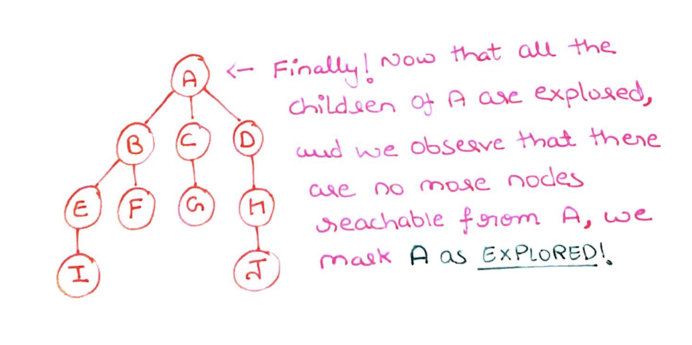
Step 20: Finally we reach node A. all the children of node A has been explored. So, we mark A as explored (red) and pop it from the stack. Completing the traversal of our graph. Step20

Algorithm - DFS:

1. Mark vertex(v) as discovered(grey)
2. Get neighbors of v. Calling each neighbor w
3. loop through neighbors:
   3.1 if neighbor is undiscovered (white)
       3.1.1 Visit  vertex w
4. Mark u as explored (black)

Time and Space complexity

In the algorithm, we are only iterating exactly for each vertex. Therefore, assuming that we have V vertices, every vertex is visited once and check the edges E of our adjacency list once, our time complexity will be O(V + E).

F(n) = Visiting vertices(V) + number of Edges(E) in adjacency list = O(V) + O(E)
	 = O(V  + E)
Back